The Gist!
- Use Big-Oh notation to describe the asymptotic running time of a program given its precise running time as a function of input size.
It turns out, in an expression like $12754n^{2} + 4353n + 834\lg n + 13546$, those constant factors will change based on how you express an algorithm.
For example, consider these three code snippets:
public void countUp(int num) {
for (int i = 1; i <= num; i++) {
System.out.println(i);
}
}
public void countUp(int num) {
int count = 1;
for (int i = 0; i < num * 2; i+=2) {
System.out.println(count++);
}
}
public void countUp(int num) {
int count = 1;
int upper = num * 2;
for (int i = 1; i <= upper; i+=2) {
System.out.println(count++);
}
}
The three programs above do the same thing (printing out numbers from $1$ to $N$ where $N$ is the value of num). So the running time of all three will be in the form of a first-degree polynomial $T(N) = aN + b$ where the coefficients $a$ and $b$ will be different for each program. In general, the coefficients (constant factors) depend on the following factors.
- How we express an algorithm.
- The programming language used to implement the algorithm
- The compiler which converts the program to machine instructions.
- The Instruction Set Architecture of the hardware it will eventually run on.
To normalize these variations, we can drop the constants (set the coefficients to $1$).
So $T_1(n) = 12754n^{2} + 4353n + 834\lg n + 13546$ becomes $T_2(n) = n^{2} + n + \lg n + 1$. We assert, $T_1(n) \propto T_2(n)$.
Moreover, when the input gets larger and larger, the highest-order term, $n^{2}$, is going to be much much larger than all the lower-order terms combined (i.e., $n + \lg n + 1$).
So, when the input gets arbitrarily large, the performance comes down to the dominant term.
Why does the dominant term dictate the performance?
The following table is from the book "Algorithm Design" by Jon Kleinberg and Eva Tardos (2006). You can see how functions' runtime grows with increasing the input size.
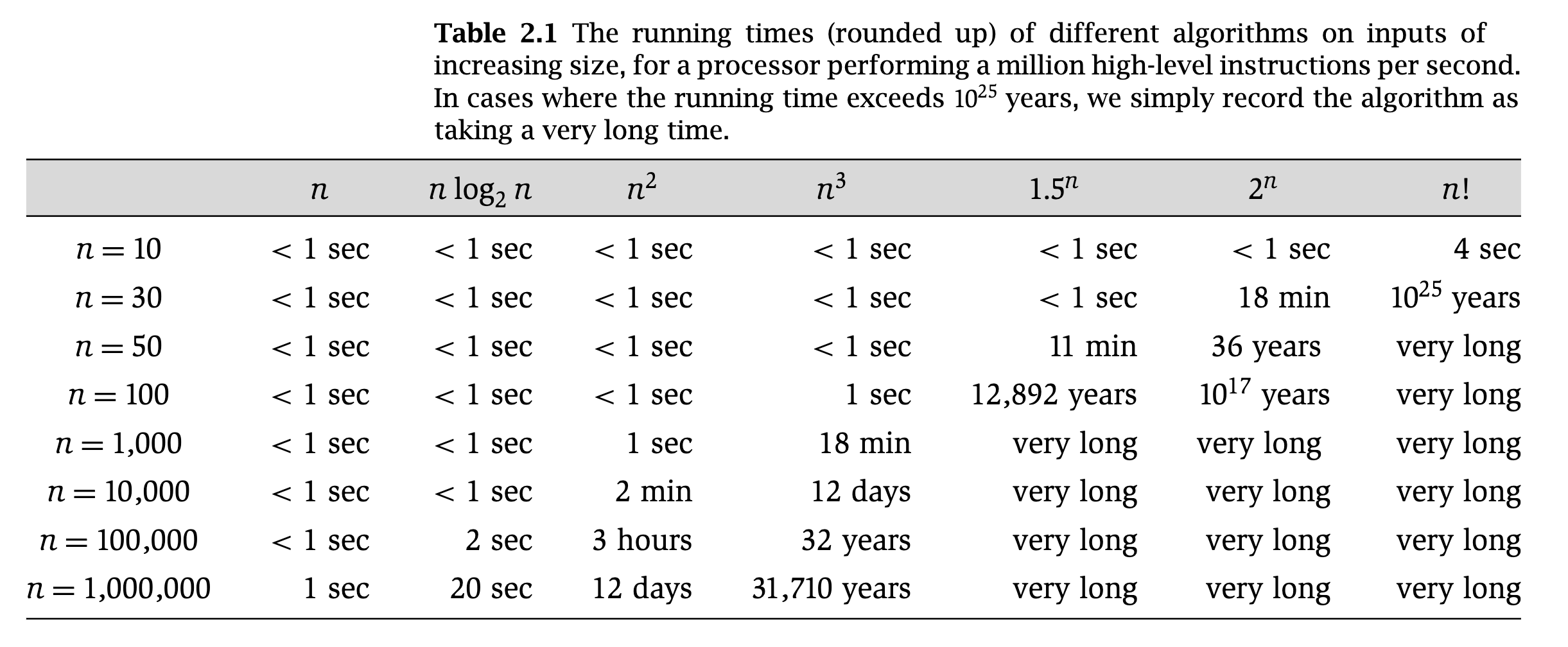
So the Big-Oh notation says:
- Suppress constant factors as they are dependent on how the algorithm is expressed.
- Ignore lower-order terms as they are irrelevant when the input gets arbitrarily large.
Resources
- freeCodeCamp has a nice article, Big O Notation — Simply explained with illustrations and video.
- Khan Academy has an article on Asymptotic notation.
- This is an interesting article: Big-O notation explained by a self-taught programmer.
- Chapter 2: Basics of Algorithm Analysis in the book "Algorithm Design" by Jon Kleinberg and Eva Tardos, 2006.