Treap Insertion: Exercise
- Select the appropriate rotation type to rebalance a Treap after performing an insertion.
Consider the following (max-heap) treap, where the keys are the letters and the priorities are the integers:

Exercise Show the result of inserting the key M, including any necessary rotations. Assume the priority generated for the key M is 15.
Solution
We insert M following the insertion process of a regular BST (ignoring priorities):

We must now apply tree rotations to fix the max-heap order property. Since M is to the left of P, we apply a right rotation to bring M above P and P to the right of M:
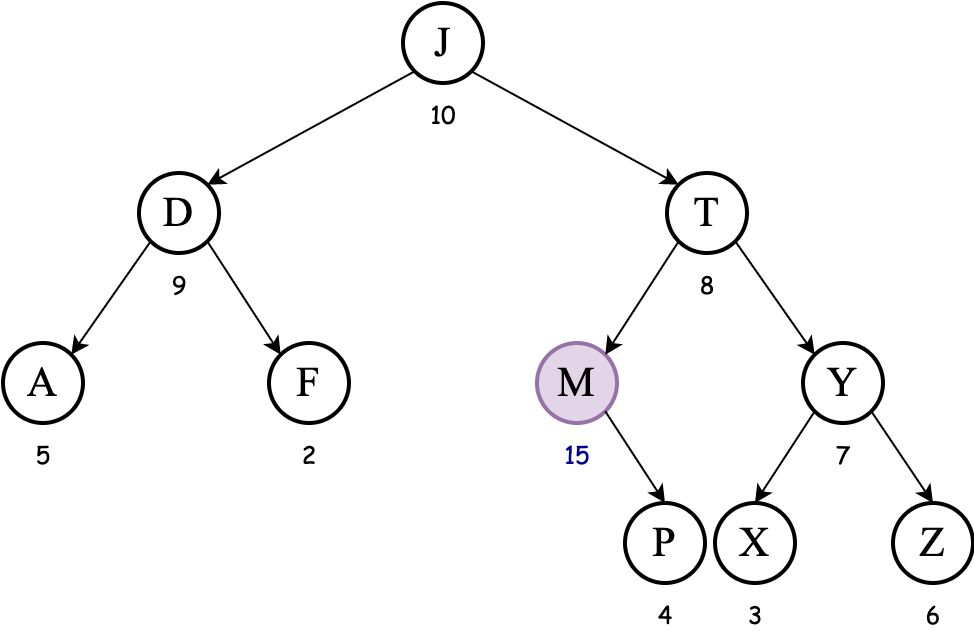
Since the priority of M is larger than the priority of T** we must apply tree rotation again to bring M above T:

We must apply a rotation one last time; this time, however, we apply a left rotation since M is to the right of J:

Notice the BST order property is maintained over the keys (letters) and the max-heap order property is maintained over the priorities (integers).