Structural Rotation: Definition
- Elaborate on the purpose of structural rotation.
Consider these numbers: $3, 5, 7$. The following are valid binary search trees made up of the given numbers. However, only one is "balanced."

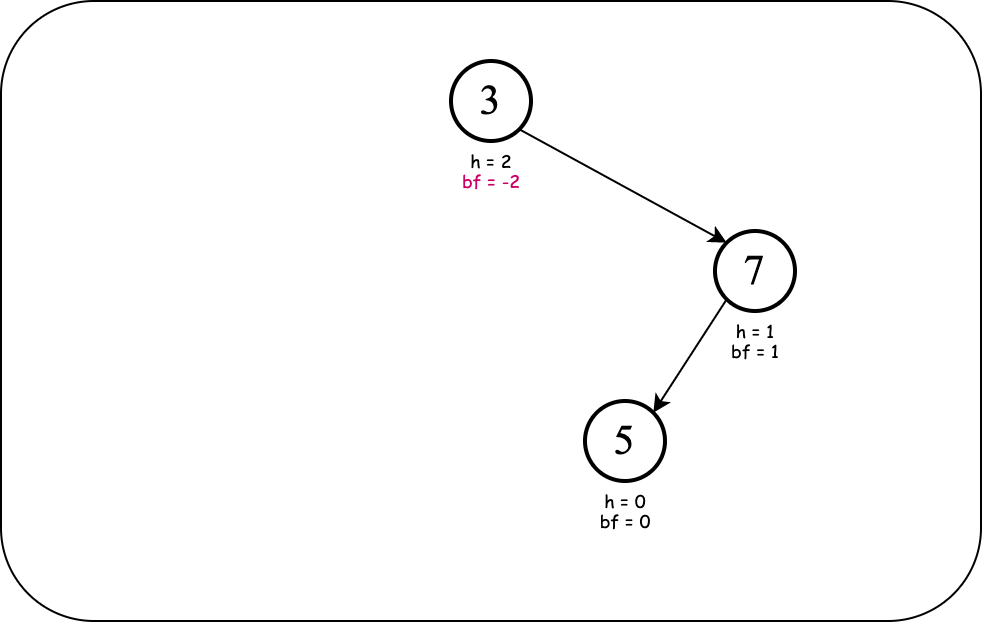
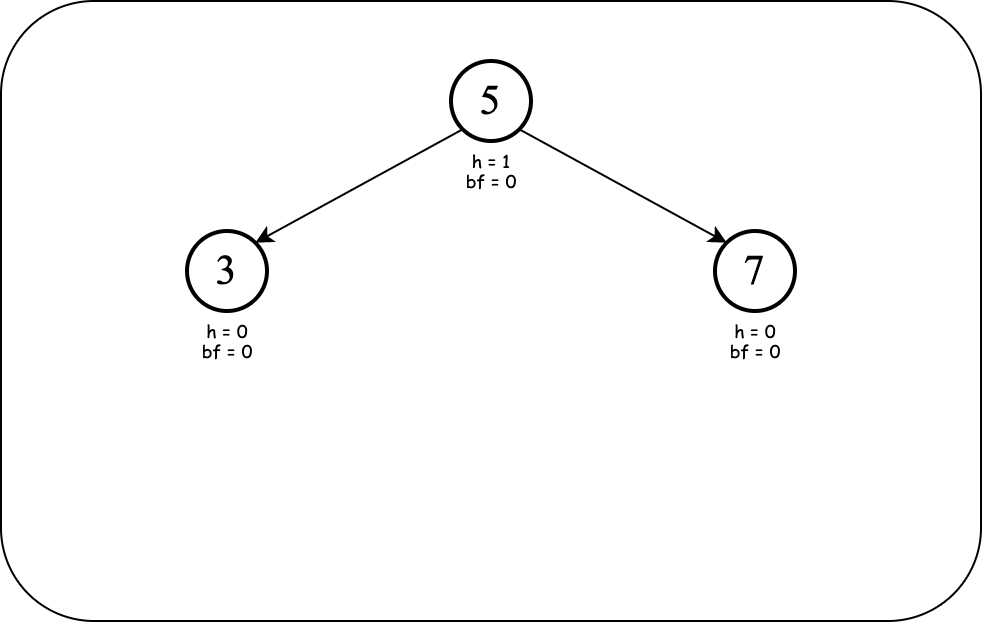
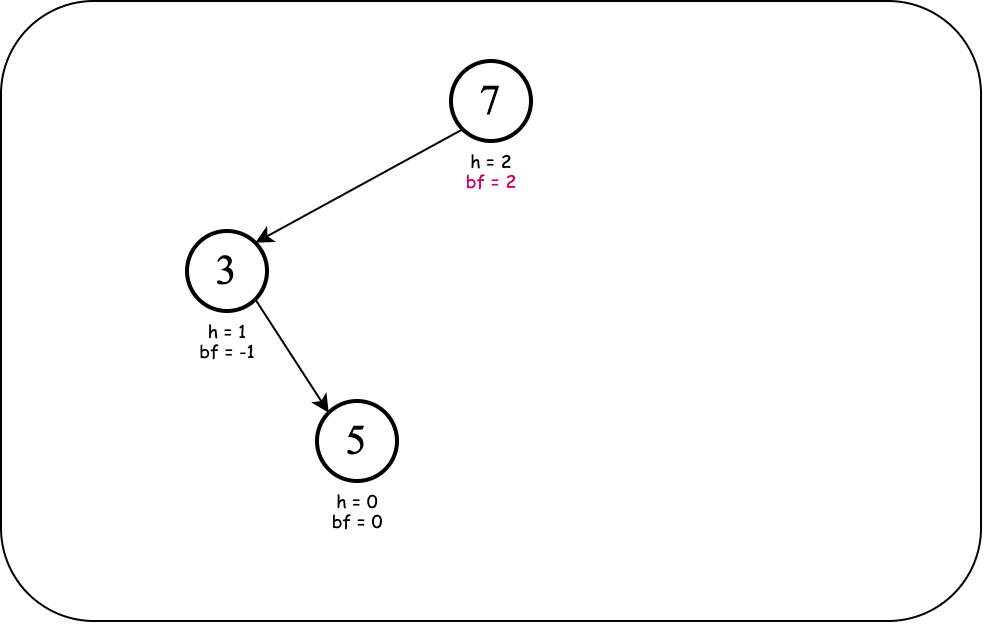

The four unbalanced trees can be transformed to the balanced one using structural rotation. (Notice the balanced one can be generated from the sequence $5, 3, 7$ or $5, 7, 3$.)
A structural rotation is an operation on a binary tree that changes the tree's structure without affecting the order of the elements (as read in by an in-order traversal).
A structural rotation is often employed to balance two branches of different depths.
In a structural rotation, one node is shifted up, another is shifted down, and some of the remaining nodes may be shifted to ensure the tree is still a binary tree (each node only has two branches).
Structural rotations change the height of the tree by moving up larger subtrees.