BST Operation: Remove (How it works)
- Explain and trace the core operations of a Binary Search Tree.
The remove operation in a BST implementation of OrderedSet ADT is a somewhat involved process! We will break it down into three scenarios.
-
Node to be removed is a leaf: Simply remove from the tree!
50 50 / \ remove(20) / \ 30 70 ---------> 30 70 / \ / \ \ / \ 20 40 60 80 40 60 80 -
Node to be removed has only one child: Copy the child value into the node and delete the child node.
50 50 / \ remove(30) / \ 30 70 ---------> 40 70 \ / \ / \ 40 60 80 60 80 -
Node to be removed has two children:
- Find the smallest value in the node's right subtree (in-order successor).
- Copy the value key of the in-order successor to the target node and delete the in-order successor.
50 60 / \ remove(50) / \ 40 70 ---------> 40 70 / \ \ 60 80 80- Note that the largest value in the left subtree (in-order predecessor) can also be used.
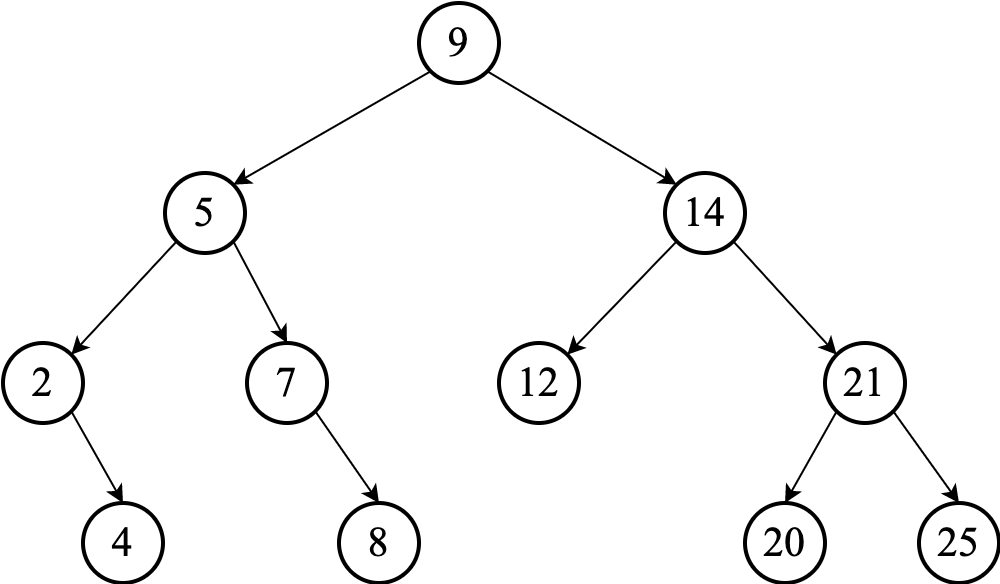
Exercise Remove $17$ from the following BST.
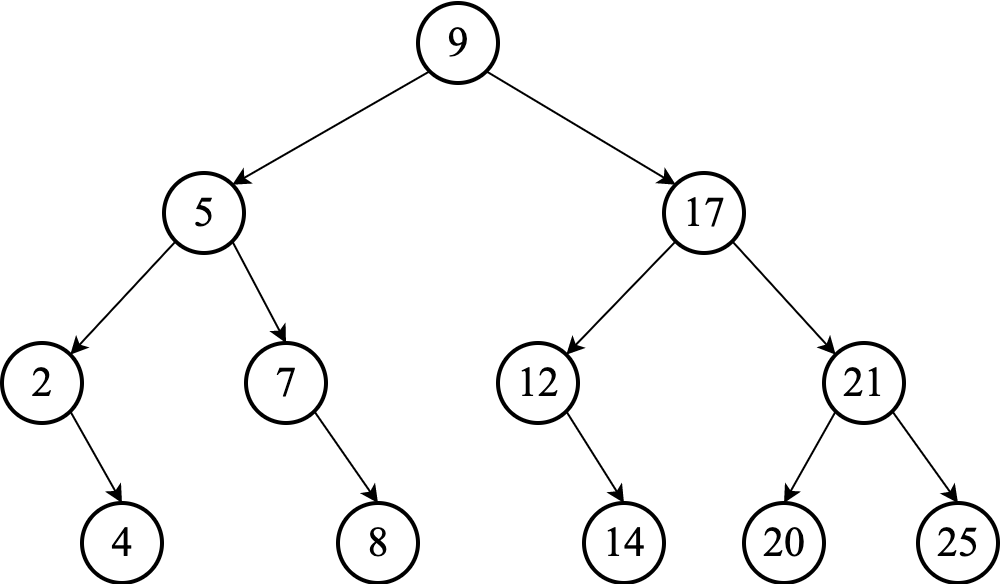
Solution
Either replace $17$ with the smallest value in its right subtree:
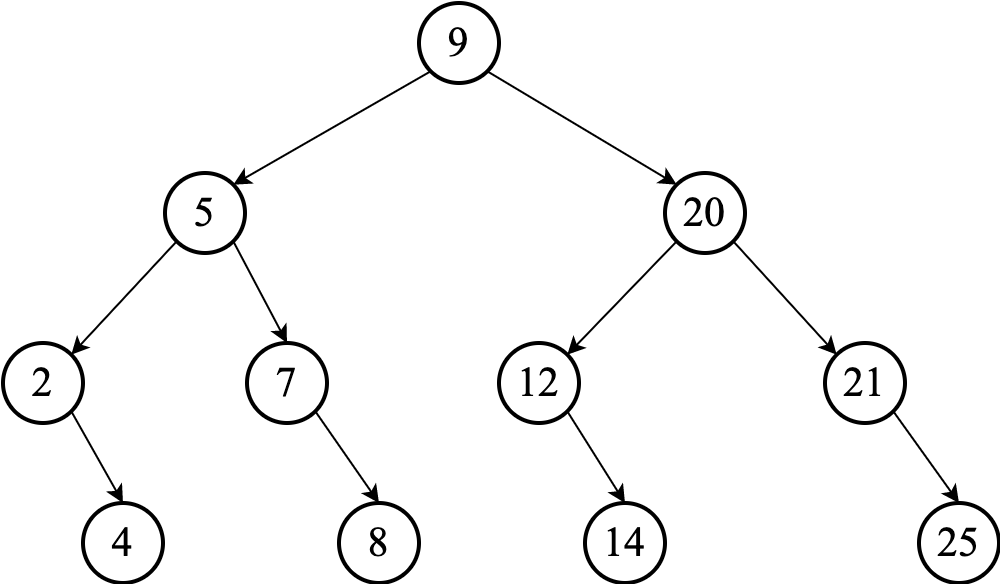
Or replace $17$ with the largest value in its left subtree: