Path
- Identify a path from a source vertex to a destination vertex.
A path is a sequence of consecutive edges in a graph.
Alternatively, we can define "path" as a sequence of vertices where each vertex in the sequence is adjacent to the vertex next to it.
Consider the following graph:
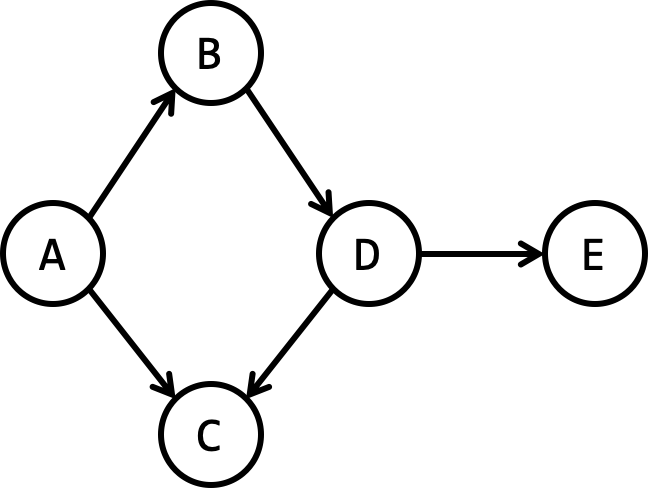
Here are two paths from $A$ to $C$: $(A, C)$ and $(A, B, D, C)$.
A simple path is a path that does not repeat any nodes or edges.
In this class, when I say "path," I mean "simple path."
Aside: In some references, what I defined as "path" is described as "walk," and instead "simple path" is called, simply, "path."
Exercise List the edges on a directed path from $B$ to $E$ and from $C$ to $E$.
Solution
- Directed path from $B$ to $E$: $((B, D), (D, E))$.
- There is no directed path from $C$ to $E$.