Motivation
- A hash table is an implementation of Set/Map aiming for average (expected) constant-time operations.
Suppose we have an array:

And we want to store a bunch of elements in it:
$$ \text{cat}, \space \text{bat}, \space \text{tap}, \space \text{mad}, \text{dam}, \space \text{nap}, \space \text{pat} $$
What will we do?
Well, we most likely store them sequentially, one after another.

Here, insertion is fast (constant time), and searching is slow (linear time).
We can get a logarithmic-time search (via binary search) if we keep the data sorted, but that means extra work for insertion (linear time).

We could organize the data in a (balanced) binary search tree to get logarithmic-time insert/remove and find.
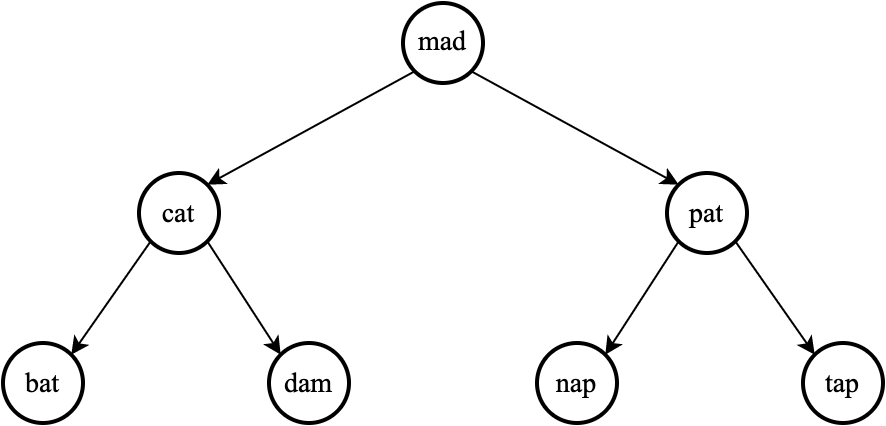
But is there any way to get constant time for all the core operations?
A hash table is a data structure aiming for average (expected) constant-time operations.