Treap: Deletion

Consider the following (max-heap) treap:

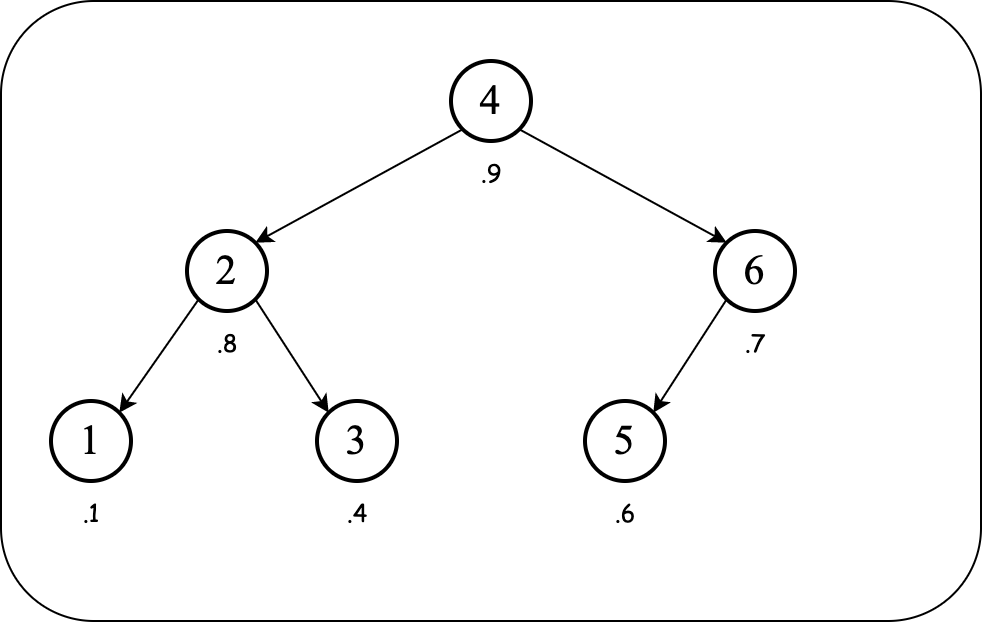
Let's remove the node with key $2$.

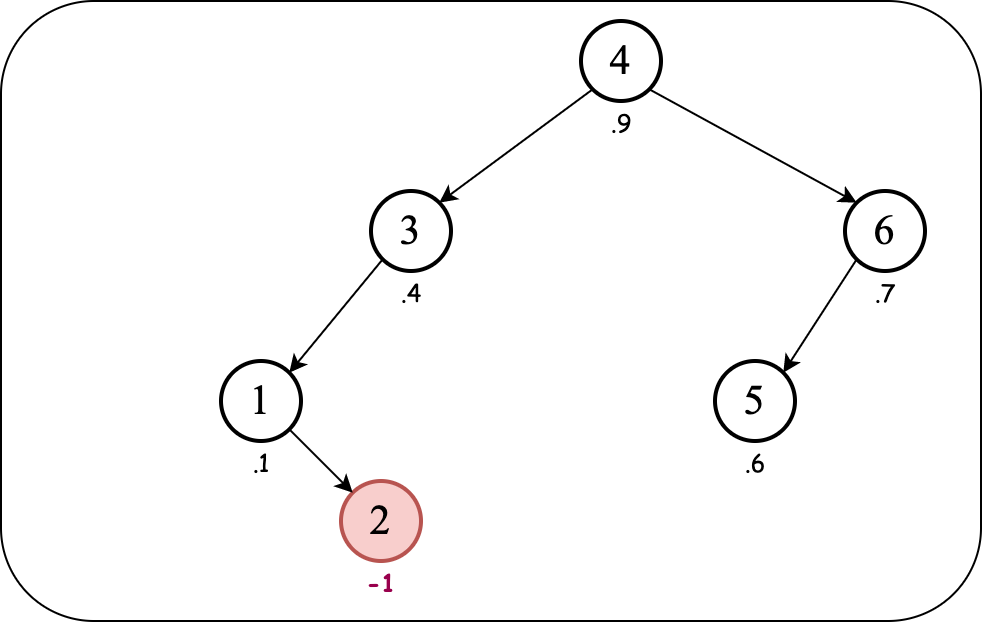
We find the entry to be removed (look-up as in BST, ignoring priorities). Since we have a "max-heap" treap and the priorities are non-negative, we set the priority of the entry to be removed to $-1$:

The max-heap order property is violated. To fix it, we need to bring the child node with key $3$ above the node with key $2$ (because $3$ has a higher priority between the children of $2$).

Since $3$ is to the right of $2$, we perform a left rotation:

The max-heap order property is still violated. To fix it, we need to bring the child node with key $1$ above the node with key $2$. Since $1$ is to the left of $2$, we perform a right rotation:

We can easily remove the node with key $2$ as it is a leaf now.

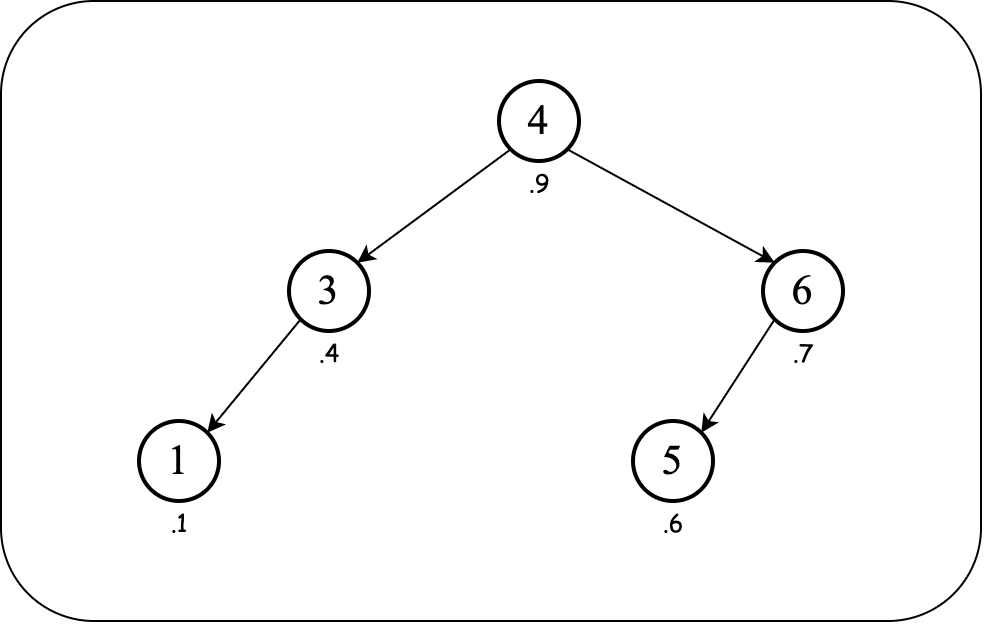
Notice the resulting treap is a BST over the keys and a max-heap over the priorities, and its height is $\Omicron(\lg n)$.