Insert Operation
- Trace the insert operation of Priority Queue with Binary Heap implementation.
Consider we have the following min-heap:
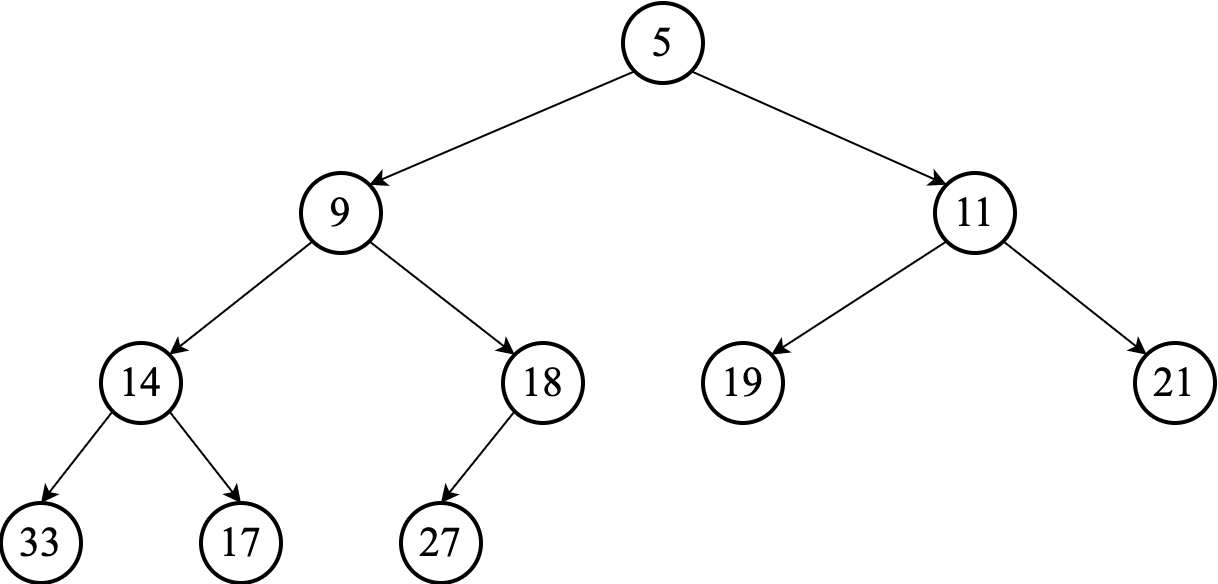
To insert a new element, such as $7$, we initially appended it to the end of the heap. (So it goes to the last level, after the last element from left to right.)
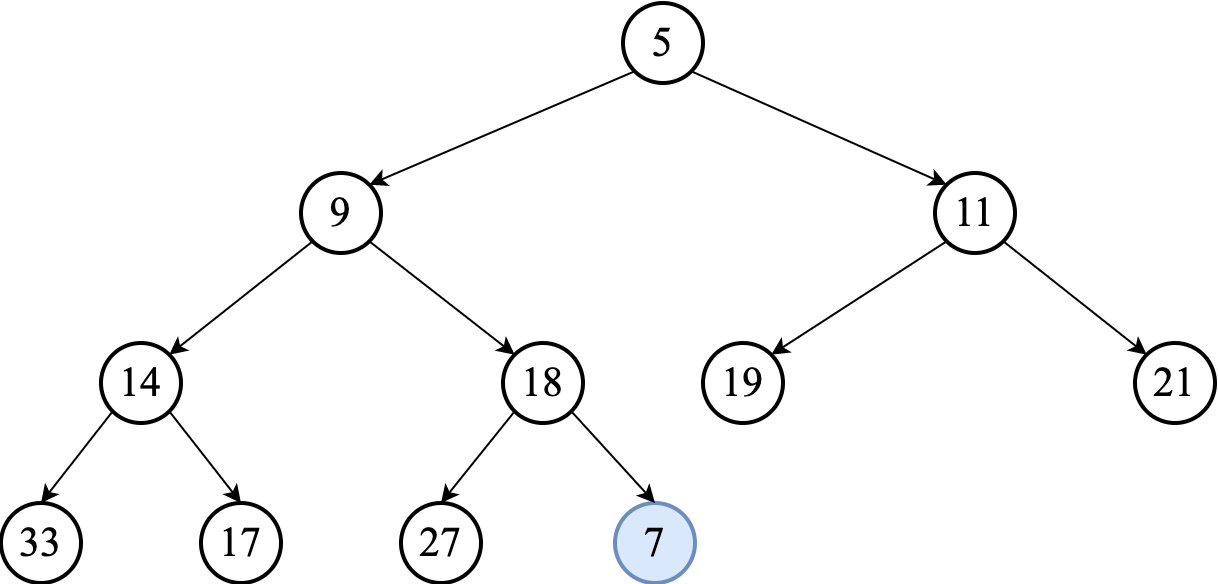
We may have to "repair" the heap property by percolating the new node to its proper position. This process is often called swim-up. It involves comparing the added element with its parent and moving it up a level (swapping with the parent) if needed.
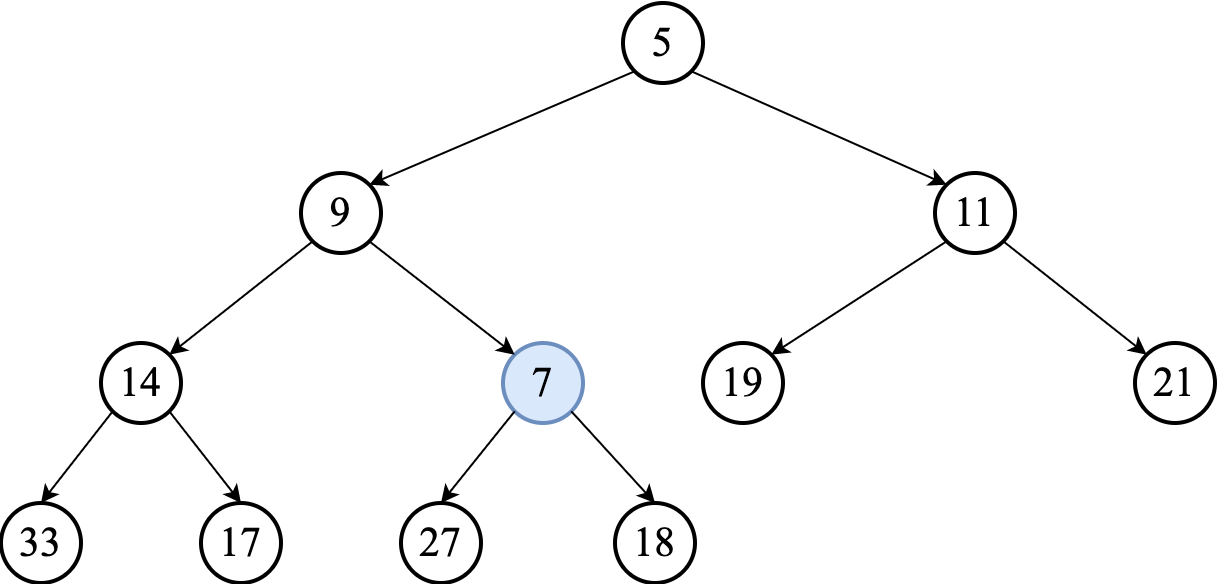
The comparison is repeated until the parent is smaller than or equal to the percolating (swimming) element.
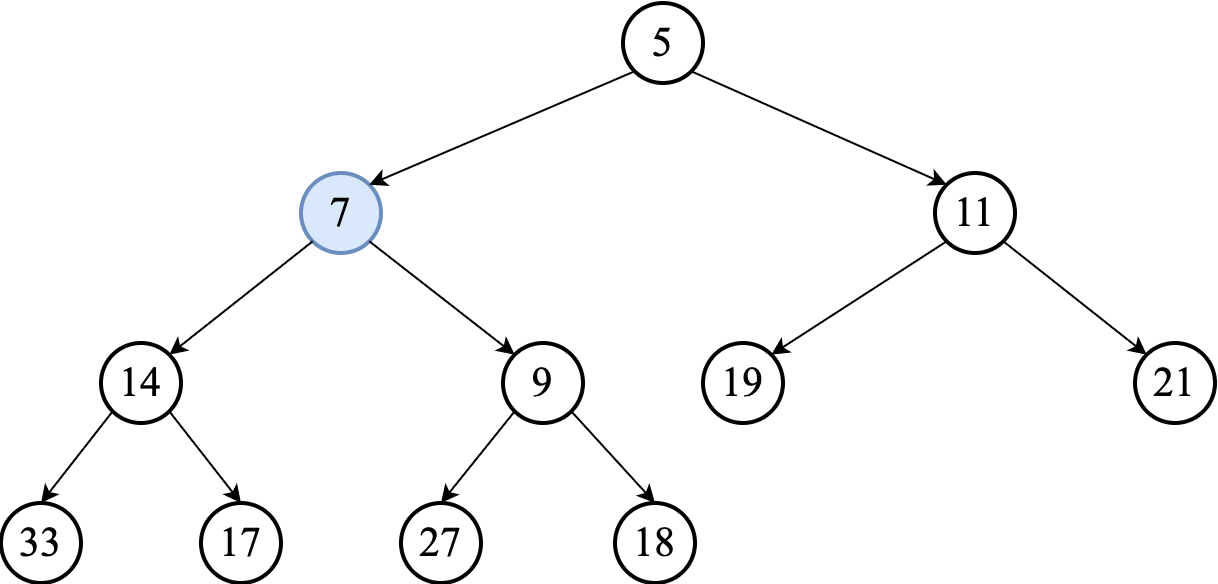
The worst-case runtime of the algorithm is $\Omicron(\lg n)$, since we need at most one swap on each level of a heap on the path from the inserted node to the root.